
- The middle note c has a frequency of 262 hertz trial#
- The middle note c has a frequency of 262 hertz plus#
This gives off hundreds of tiny pressurised air pockets which travel through the atmosphere in waves of sound towards our ears. When a musical note is played for example, on a guitar, the string of the guitar vibrates. According to Rosenthal (2005) ‘Musical notations as octaves, chords, scales and keys can all be demystified and understood logically using simple mathematics’.īut how does music work? And where do maths and music meet? Or perhaps they did not realize that the last jump at B would take them to F♯, not F.Believe it or not, there are many mathematical concepts which permeate music. Since the author (or authors) of Intervals and Notation jumped up 4 fifths, what they probably did was start at the A flat (A♭) position on the circle by mistake. Stepping down 6 octaves gives us a value in the desired range. Acccording to the circle of fiths, to get to C from A requires a jump of 9 fifths up. Therefore, Middle C is at a frequency of 278.4375 Hz Raise a fifth to F-immediately-above-middle-C Lower one octave to B-immediately-below-middle-C Raise a fifth to B-almost-an-octave-above-middle-C Raise a fifth to E-more-than-an-octave-above-middle-C The student who wrote the essay above cites a page called Intervals and Notation that claims that C can be generated from A by the following procedure… A-almost-an-octave-above-middle-C is at

The order in which this method generates notes is written clockwise around the circumference of a circle thus the name "circle of fifths".
The middle note c has a frequency of 262 hertz plus#
Keep repeating this over and over again until you have all twelve notes of the European chromatic scale - the 7 notes corresponding to the letters A through G plus 5 extra notes midway between the original 7 indicated with the addition of a sharp (♯) or flat (♭) symbol. Multiplying and dividing by two changes the octave of the note. If the resulting note is too high, divide it by two. Start with a note you like and multiply it by 3/2. The circle of fifths is a method for generating a musical scale that is often credited to the Classical Greek mathematician Pythagoras. In general, the frequency of middle C is between 256 Hz and 280 Hz.ĭanielle Daly - 2003 Bibliographic Entry In order to find the frequency of a note one octave lower the frequency is halved.
The middle note c has a frequency of 262 hertz trial#
The frequency for one trial comes out to be 262 Hz because the frequency of the C one octave higher than middle C in that scale is 524 Hz. Since each scale has a different frequency for middle C, the frequency has also been known as 262 Hz, 256 Hz, and 264 Hz. A different set of ratios and a different fixed pitch will result in a different value for middle C. Scales are built on ratios and fixed notes. For example just intonation, equal temperament, mean tempered, American standard, and international standard. The frequency of middle C turns out to be 278.4375 Hz. Follow the octave going up and down where needed. To find the frequency of a note one octave lower the frequency is halved.įrequency can also go in fifths by using the formula x(3/2) = y where x is the original note and y is the fifth note above the original. To find the frequency of a note an octave higher the frequency is doubled. The middle A, above middle C, has a frequency of 440 Hz. It goes C, D, E, F, G, A, B, C, and continues up and down on a standard musical instrument. In music there is an octave that is made up of eight notes.
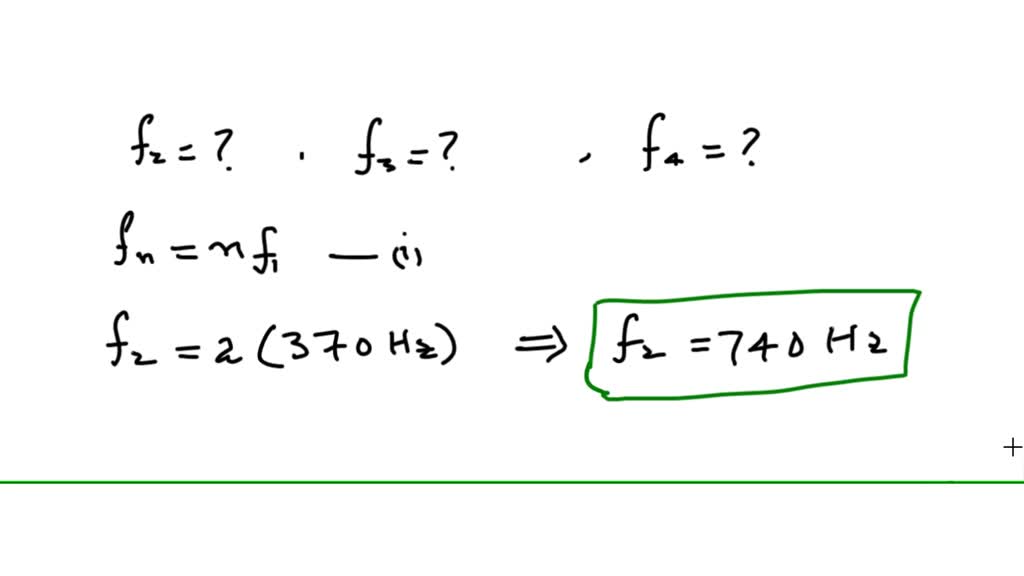
"The note musicians call Middle C has a frequency of 262Hz." "Some scientific manufacturers once adopted a standard of 256 Hz for middle C, but musicians ignored it." Synthesizers, Music & BroadcastingĬulver, C. "Playing middle C on the piano keyboard produces a sound with a frequency of 256 Hz."


 0 kommentar(er)
0 kommentar(er)
